Degrees of visual angle

You will often see that the size of visual stimuli is expressed in degrees of visual angle (°). Visual degrees express the angle between the straight lines from the extremities of the stimulus to the eye's lens. Therefore, visual angle is related to the size that a stimulus subtends on the retina, but only indirectly: It is an angle measured from the eye's lens, as illustrated in Figure 1

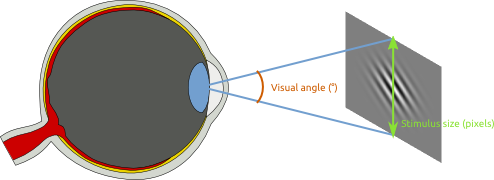
Figure 1. A schematic illustration of degrees of visual angle. (Image adapted from WikiMedia Commons.)

The reason for using this somewhat odd measure of size is that it reflects the perceived size of a stimulus, which in psychological experiments is often more important than its real size. For example, if you present a picture with a real width of 100 pixels on the monitor, the visual angle may correspond to 3°. If you move the monitor further away, the visual angle of the picture will decrease to, say, 2°. Visual angle thus reflects that the distance between a stimulus and an observer is important.

See also:

• http://en.wikipedia.org/wiki/Visual_angle

Convert pixels to visual degrees

You will need to know three things in order to convert pixels to visual degrees:

• h is the height of the monitor in centimeters, which you can measure with a ruler. (e.g., 25cm)
• d is the distance from the participant to the monitor in centimeters, which you can measure with a ruler. (e.g., 60cm)
• r is the vertical resolution of the monitor in pixels, which you can find in your operating system's display settings (e.g., 768 px)

You can calculate angular size of your stimulus as shown in Listing 1. You can execute this script in the OpenSesame debug window. Of course, you need to substitute all values so that they correspond to your setup. Note that a single visual degree typically corresponds to 30 - 60 pixels, depending on the distance and size of the monitor. Conversely, a single pixel typically corresponds to 0.01 to 0.03 visual degrees. If you obtain values that are far outside of this range, you have probably made a mistake.

from math import atan2, degrees
h = 25 # Monitor height in cm
d = 60 # Distance between monitor and participant in cm
r = 768 # Vertical resolution of the monitor
size_in_px = 100 # The stimulus size in pixels
# Calculate the number of degrees that correspond to a single pixel. This will
# generally be a very small value, something like 0.03.
deg_per_px = degrees(atan2(.5*h, d)) / (.5*r)
print '%s degrees correspond to a single pixel' % deg_per_px
# Calculate the size of the stimulus in degrees
size_in_deg = size_in_px * deg_per_px
print 'The size of the stimulus is %s pixels and %s visual degrees' \
    % (size_in_px, size_in_deg)

Convert visual degrees to pixels

Converting visual degrees to pixels is simply the inverse of the procedure described above, and can be done as shown in Listing 2.

from math import atan2, degrees
h = 25 # Monitor height in cm
d = 60 # Distance between monitor and participant in cm
r = 768 # Vertical resolution of the monitor
size_in_deg = 3. # The stimulus size in pixels
# Calculate the number of degrees that correspond to a single pixel. This will
# generally be a very small value, something like 0.03.
deg_per_px = degrees(atan2(.5*h, d)) / (.5*r)
print '%s degrees correspond to a single pixel' % deg_per_px
# Calculate the size of the stimulus in degrees
size_in_px = size_in_deg / deg_per_px
print 'The size of the stimulus is %s pixels and %s visual degrees' \
    % (size_in_px, size_in_deg)